NS - Pillole di elettrotecnica: Flusso del campo elettrico

NihilScio

Educational search engine -

Per capire devi anche sapere

Cariche elettriche
Campo elettrico
Funzioni trigonometriche

Flusso del campo elettrico

Dato un campo elettrico di intensità E e fissata una determinata superficie S all’interno del suddetto campo, si definisce flusso del campo elettrico il vettore risultante dal prodotto ExS avente modulo:

F=E S cosa

Concetto di flusso

Nel linguaggio comune la parola flusso è quasi sempre associata alla quantità di materia, in genere fluido, che scorre in un tubo o in un canale.

Volendo fare una misura del flusso di un fluido, la cosa migliore da fare è fissare una determinata sezione normale al tubo e misurare quanta materia passa attraverso di essa in un secondo.

In pratica di troverà che passa tanta più materia quanto più grande è l’area della superficie fissata e quanto più alta è la velocità del fluido.

Analogamente si può dire che, dato un campo elettrico di intensità E, e fissata una superficie S in una zona dello spazio, il flusso del campo elettrico è rappresentato dal numero di linee di forza del campo che attraversano la suddetta superficie.

Ovviamente l’analogia non è perfetta perché non si considera alcun movimento di materia o di cariche e pertanto il tempo nella misura del flusso non viene preso in considerazione. Brevemente il valore del flusso può essere calcolato come prodotto dell’intensità del campo elettrico per l’area della superficie considerata:

F=ES

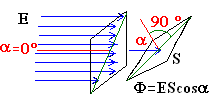
In questa formula il valore S della superficie assume fondamentale importanza. Infatti il numero delle linee di forza, che attraversa la superficie, cambia in funzione dell’inclinazione della superficie rispetto alla direzione del campo. Come si vede dalla figura, se l’angolo di incidenza del vettore campo è diverso da 90 alcune linee di forza non attraversano la superficie e quindi il valore del flusso a parità di intensità del campo elettrico diminuisce. Per tener conto di questo fatto occorre correggere la suddetta formula nel seguente modo:

F=EScos a

Ove a è l’angolo tra la direzione del campo E e la normale alla superficie S. Essendo E=Volt/metro e S=m², dimensionalmente il flusso si può esprimere come:
V
F= ---- m² = V x m
m

Roberto Iuppariello

Dato un campo elettrico di 15V/m avente direzione normale ad una superficie rettangolare S di dimensioni 3 e 5 cm, si determini il flusso.
Si determini il flusso, con i dati del precedente esercizio, supponendo la direzione del campo inclinata di 45° rispetto alla normale alla superficie.
Si calcoli l'area di una superficie perpendicolare ad un campo elettrico uniforme di intensità 10V/m che determina un flusso di 5Vm
Si determini l'intensità del campo elettrico che attraverso una superficie di 0,5m²inclinata di 30° rispetto ad esso, determina un flusso di 4Vm
Si determini la direzione del campo di 10V/m che determina un flusso di 1,5Vm su una superficie di 30 cm².